Petersen graph: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{particular undirected graph}} | {{particular undirected graph}} | ||
[[File:Petersen graph.svg|thumb|300px|right|the Petersen graph is typically drawn as a pentagon with a pentagram inside.]] | |||
[[File:Kneser graph KG(5,2).svg|thumb|300px|right|the Petersen graph as KG(5,2). The subsets corresponding to each vertex are indicated in the bubble for that vertex.]] | |||
==Definition== | ==Definition== | ||
| Line 6: | Line 7: | ||
# It is the [[defining ingredient::complement of a graph|complement]] of the [[defining ingredient::line graph]] of [[defining ingredient::complete graph:K5]]. | # It is the [[defining ingredient::complement of a graph|complement]] of the [[defining ingredient::line graph]] of [[defining ingredient::complete graph:K5]]. | ||
# It is the [[defining ingredient::Kneser graph]] <math>KG_{5,2}</math>: its vertices are identified with subsets of size two of a 5-element set, and two vertices are adjacent if and only if the corresponding subsets are disjoint. | # It is the [[defining ingredient::odd graph]] with parameter 3, i.e., the graph <math>O_3</math>. Explicitly, this is the [[defining ingredient::Kneser graph]] <math>KG_{5,2}</math>: its vertices are identified with subsets of size two of a 5-element set, and two vertices are adjacent if and only if the corresponding subsets are disjoint. | ||
# It is the unique 5-[[defining ingredient::cage]]. | # It is the unique (3,5)-[[defining ingredient::cage]]. | ||
==Arithmetic functions== | |||
===Size measures=== | |||
{| class="sortable" border="1" | |||
! Function !! Value !! Explanation | |||
|- | |||
| {{arithmetic function value|size of vertex set|10}} || As <math>O_n, n = 3</math>: <math>\binom{2n - 1}{n - 1} = \binom{5}{2} = 10</math> | |||
|- | |||
| {{arithmetic function value|size of edge set|15}} || As <math>O_n, n = 3</math>: <math>\frac{1}{2} \binom{2n - 1}{n - 1,n - 1,1} = \frac{1}{2} \binom{5}{2,2,1} = 15</math> | |||
|} | |||
===Numerical invariants associated with vertices=== | |||
Since the graph is a [[vertex-transitive graph]], any numerical invariant associated to a vertex must be equal on all vertices of the graph. Below are listed some of these invariants: | |||
{| class="sortable" border="1" | |||
! Function !! Value !! Explanation | |||
|- | |||
| {{arithmetic function value|degree of a vertex|3}} || As <math>O_n, n = 3</math>: <math>n = 3</math> | |||
|- | |||
| {{arithmetic function value|eccentricity of a vertex|2}} || As <math>O_n, n = 3</math>: <math>n - 1 = 2</math> | |||
|} | |||
===Other numerical invariants=== | |||
{| class="sortable" border="1" | |||
! Function !! Value !! Explanation | |||
|- | |||
| {{arithmetic function value|clique number|2}} || As <math>O_n, n = 3</math>: 2, since <math>n \ge 3</math> | |||
|- | |||
| {{arithmetic function value|independence number|4}} || {{fillin}} | |||
|- | |||
| {{arithmetic function value|chromatic number|3}} || | |||
|- | |||
| {{arithmetic function value|radius of a graph|2}} || Due to vertex-transitivity, the radius equals the eccentricity of any vertex, which has been computed above. | |||
|- | |||
| {{arithmetic function value|diameter of a graph|2}} || Due to vertex-transitivity, the radius equals the eccentricity of any vertex, which has been computed above. | |||
|- | |||
| {{arithmetic function value|odd girth|5}} || As <math>O_n ,n = 3</math>: <math>2n - 1 = 2(3) - 1 = 5</math> | |||
|- | |||
| {{arithmetic function value|even girth|6}} || As <math>O_n, n = 3</math>: 6 (we use that <matH>n \ge 3</math>) | |||
|- | |||
| {{arithmetic function value|girth of a graph|5}} || As <matH>O_n, n = 3</math>: <math>\min \{ 2n - 1,6 \}</math> | |||
|} | |||
==Graph properties== | |||
{| class="sortable" border="1" | |||
! Property !! Satisfied? !! Explanation | |||
|- | |||
| [[satisfies property::connected graph]] || Yes || all odd graphs are connected. More generally, all Kneser graphs <math>KG_{m,k}</math> are connected for <math>k < m/2</math>. | |||
|- | |||
| [[satisfies property::regular graph]] || Yes || all odd graphs, and more generally all [[Kneser graph]]s, are regular | |||
|- | |||
| [[satisfies property::vertex-transitive graph]] || Yes || all odd graphs, and more generally all [[Kneser graph]]s, are vertex-transitive | |||
|- | |||
| [[satisfies property::strongly regular graph]] || Yes || This follows on account of it being a Kneser graph of the form <math>KG_{m,2}</math>, i.e., the key is that the subset sizes are 2 | |||
|- | |||
| [[satisfies property::edge-transitive graph]] || Yes || | |||
|- | |||
| [[satisfies property::symmetric graph]] || Yes || | |||
|- | |||
| [[satisfies property::distance-transitive graph]] || Yes || | |||
|- | |||
| [[dissatisfies property::self-complementary graph]] || No || The degree is 3 and the number of vertices is 10. For the graph to be self-complementary, a necessary condition is that the number of vertices should be 1 + twice the degree | |||
|- | |||
| [[satisfies property::cubic graph]] || Yes || The degree of every vertex is 3, as computed above. | |||
|- | |||
| [[satisfies property::bridgeless graph]] || Yes || | |||
|- | |||
| [[satisfies property::cage]] || Yes || | |||
|- | |||
| [[satisfies property::snark]] || Yes || | |||
|} | |||
Latest revision as of 21:21, 23 December 2012
This article defines a particular undirected graph, i.e., the definition here determines the graph uniquely up to graph isomorphism.
View a complete list of particular undirected graphs
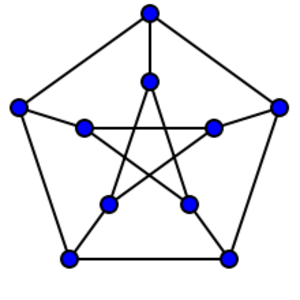
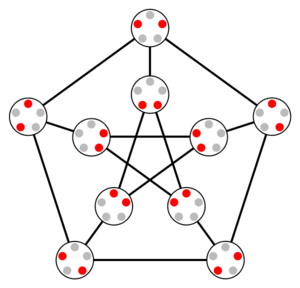
Definition
The Petersen graph is a particular undirected graph on 10 vertices that can be defined in the following equivalent ways:
- It is the complement of the line graph of complete graph:K5.
- It is the odd graph with parameter 3, i.e., the graph . Explicitly, this is the Kneser graph : its vertices are identified with subsets of size two of a 5-element set, and two vertices are adjacent if and only if the corresponding subsets are disjoint.
- It is the unique (3,5)-cage.
Arithmetic functions
Size measures
| Function | Value | Explanation |
|---|---|---|
| size of vertex set | 10 | As : |
| size of edge set | 15 | As : |
Numerical invariants associated with vertices
Since the graph is a vertex-transitive graph, any numerical invariant associated to a vertex must be equal on all vertices of the graph. Below are listed some of these invariants:
| Function | Value | Explanation |
|---|---|---|
| degree of a vertex | 3 | As : |
| eccentricity of a vertex | 2 | As : |
Other numerical invariants
| Function | Value | Explanation |
|---|---|---|
| clique number | 2 | As : 2, since |
| independence number | 4 | Fill this in later |
| chromatic number | 3 | |
| radius of a graph | 2 | Due to vertex-transitivity, the radius equals the eccentricity of any vertex, which has been computed above. |
| diameter of a graph | 2 | Due to vertex-transitivity, the radius equals the eccentricity of any vertex, which has been computed above. |
| odd girth | 5 | As : |
| even girth | 6 | As : 6 (we use that ) |
| girth of a graph | 5 | As : |
Graph properties
| Property | Satisfied? | Explanation |
|---|---|---|
| connected graph | Yes | all odd graphs are connected. More generally, all Kneser graphs are connected for . |
| regular graph | Yes | all odd graphs, and more generally all Kneser graphs, are regular |
| vertex-transitive graph | Yes | all odd graphs, and more generally all Kneser graphs, are vertex-transitive |
| strongly regular graph | Yes | This follows on account of it being a Kneser graph of the form , i.e., the key is that the subset sizes are 2 |
| edge-transitive graph | Yes | |
| symmetric graph | Yes | |
| distance-transitive graph | Yes | |
| self-complementary graph | No | The degree is 3 and the number of vertices is 10. For the graph to be self-complementary, a necessary condition is that the number of vertices should be 1 + twice the degree |
| cubic graph | Yes | The degree of every vertex is 3, as computed above. |
| bridgeless graph | Yes | |
| cage | Yes | |
| snark | Yes |